為什麼想做這一個題目
因為一部電影星際效應,裡面主角要去尋找另一個適合人類生存的星球,有些星球位於鄰近黑洞的地方,他們越靠近,到達那個星球,他們時間就會變得越慢。他們自身並沒有發覺時間變慢,他們在那個星球上待幾個小時,但是相對的在遠方等著他們回來的夥伴卻已經歷經好幾十年的歲月了。而當他再回去找到他女兒時,他女兒竟然已經變成比他還老的奶奶了!
因為這個問題所以我開始想了解這是為什麼?漸漸的就去了解到相對論。
相對論的兩個基本假設
科學家測光沿著地球轉向的速度,以及光逆著地球轉向的速度,按古典的觀念來說,沿著地球轉向時原本的光速加上地球轉速測得的值應該會比光速要快,而逆著地球轉向測得的值會比光速小,但實驗結果卻是兩邊光速都一模一樣。
我們無法真的知道每個座標系誰是靜止誰是運動中的。也就是說物理定律在一切參考系中都具有相同的形式。
勞倫茲變換
在兩個等速直線相對運動的座標系(慣性座標系),維持光速在各座標皆相同所需要的時空變換。
時間膨脹
等速運動的物體帶在身上的時鐘,用靜系觀察者的時鐘去測量,不論運動方向,測量結果「動鐘」都隨著運動速度增加而變慢。
- 光速運動的物體(如光子),它的時間是靜止的。
- 速度低於光速的物體,其時間膨脹的程度遵循洛侖茲變換:

長度收縮
對某運動物體進行觀測,在運動的那個方向,長度會比相對於物體靜止的觀測者觀測到的同一長度要短。

相對論質量

m0指絕對質量(及牛頓力學中的質量),m為相對論質量。
由公式可以看出:
- 對於一個有質量的物體,其速度v不可能等於或者超過光速,否則分母將會無意義或為一個虛數(註:光子沒有質量,因此其速度可以達到光速)。
- 當某有質量之物體移動速率越接近光速,相對論質量會變重。
- 當v遠小於c時,m近似於m0,符合牛頓力學定律。
解釋時間膨脹
 甲觀察者在車廂內時
甲觀察者在車廂內時
圖一
- 當甲觀察者在內部時,光源從A點射出,到達B點為一秒30萬公里,並折回來,總共是兩秒。
- 甲會觀察到光線是直線來回。
 乙觀察者在車廂外時
乙觀察者在車廂外時
圖二
- 當乙觀察者站在車廂外,車由左至右行駛,乙會看到光線往右上方射出,再往右下折返,形成一個三角形的軌跡。
- 圖二的A點跟B點距離變長,但是根據相對論光速還是必須以每秒三十萬公里速度前進,所以必須要時間膨脹,才能使的光速都保持在每秒三十萬公里的速度前進。
計算
只有透過勞倫茲變換公式的時間膨脹效應,才可以使光速在不同的慣性座標系之下,都還是維持每秒三十萬公里。
假設車廂高度 30 萬公里,車廂以 光速相對月台前進。甲觀察者在車廂內,看到光自車廂底射向車廂頂歷時一秒,從車箱頂再反射回車廂底又歷時一秒(如圖一),光速恰為每秒 30 萬公里。
光速相對月台前進。甲觀察者在車廂內,看到光自車廂底射向車廂頂歷時一秒,從車箱頂再反射回車廂底又歷時一秒(如圖一),光速恰為每秒 30 萬公里。
現在乙觀察在月台上,看到光的軌跡如圖二,依下列步驟進行計算,驗證乙觀察者測得的光速。
- 時間由1秒膨脹到1.34秒:

- 每秒20萬公里為
 光速,時間膨脹到1.34秒後,車廂前進
光速,時間膨脹到1.34秒後,車廂前進  為26.8萬公里 :
為26.8萬公里 : (萬)
(萬)
- 斜邊
 的平方為
的平方為  (萬萬)
(萬萬)
- 時間膨脹到1.34秒,光走了斜邊
 40.227萬公里:
40.227萬公里:
- 月台觀察到光軌跡的速度=距離/時間,光速還是接近於30萬公里:

再將車廂與月台的相對速度推廣到任意速度
推廣到任意速度 。
。
- 時間由1秒膨脹為
 秒
秒 秒
秒

- 斜邊

- 斜邊

- 光速=斜邊/經過時間=

長度收縮
- 高速下的時空
- 當一個物體以接近光速運動時,延運動方向的長度會比相對於物體靜止狀態觀測者觀察到的還短。
以「穀倉-竿弔詭」(房子-梯子)解釋長度收縮
- 假設有一個靜止不動的穀倉,前門打開,後門關閉,穀倉總長3公尺。有一個超人類帶著一根長3.1公尺的木棍以光速衝向穀倉。當超人類經過穀倉的時候,以古典的觀念木棍會有超過穀倉的部份,但是因為超人類是以光速前進,穀倉是靜止的,所以木棍因為長度收縮效應變短了,觀察者會看到木棍有一段時間是可以完全在穀倉內部。
 梯子與房子都靜止時 梯子與房子都靜止時 |
 觀察者在房中,看到房子靜止,梯子因運動而縮短 觀察者在房中,看到房子靜止,梯子因運動而縮短 |
 觀察者與梯子同步,看到的是房子縮短而梯子未縮短 觀察者與梯子同步,看到的是房子縮短而梯子未縮短
|
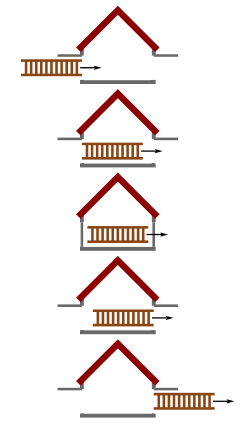 「動」梯通過「靜」房示意圖
「動」梯通過「靜」房示意圖
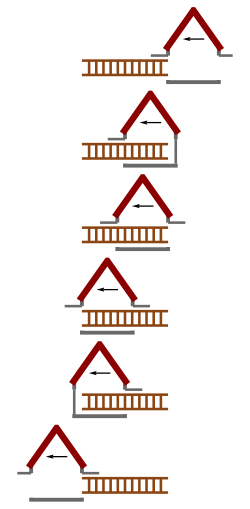 「動」房通過「靜」梯示意圖
「動」房通過「靜」梯示意圖
- 此案例中包含兩個事件:甲事件是梯子前端到達房子後門,乙事件是梯子尾端到達房子前門。
- 梯子長度的定義是:在選定的座標系中,同時量取頭尾、兩點座標,所得的座標差,即其長度。
- 在房子靜止的例子中,甲、乙事件是同時的,我們同時量取甲乙事件的座標差,因運動中的長度收縮,運動梯子的長度會小於靜止梯子的長度,所以可以擠進房子裡。而在梯子擠進房子時,同時關上房子的前後門,然後瞬間再打開前後門,讓梯子穿出房子。
- 在房子運動的例子中,房子的寬度也縮短了,但甲、乙事件不同,持梯的人看到的是梯子前端「先」到達房子後門(第三格),然「後」才發生梯子尾端到達房子前門(第四格)。
- 一般人會發生錯覺而難解,是因為認為「甲、乙事件如果在一個座標系中同時,也會在其他座標系中同時」。但在相對論中沒這回事。
- 關閉右側門竿的長度收縮圖示
上面連結所示圖中的右側的門是關著的。長棍因為高速運動已經長度縮短了,當棍子的前端接觸到關閉的門,無法再前進時,棍子前端就必須傳送訊息通知後端不能繼續前進,但前端發送訊息至後端也要一段時間,在那段時間後端依然還在繼續前進。
相對論質量
在狹義相對論中,質量並不守恆,而是「質能守恆」,所以相對論質量必須定義成一個依速度而變化的量。
這個動態質量的定義,不能有「每輸入一單位能量就能提高固定速度」的特性,否則一定會將質點加速超過光速,應該要有「質點速度越大,每輸入一單位能量所得到的速度增加越小,且無法加速到超過光速」的特性。
將相對論質量定義為:
- 當 v 為 0 時,m=m0為靜止質量。
- 這個質量定義會導出
 ,而此推論也已在實驗中多次獲得驗證了。
,而此推論也已在實驗中多次獲得驗證了。
推導過程
定義:
- 速度

- 動量

- 力

- 動能


(一)由定義 1,2,3,4 得出動能差為 d(m*v)*v
 ,因為
,因為 
 ,因為
,因為 
 ,因為
,因為 
(二)得出動能差為 
由上一段得 第①式
第①式
(三)用相對論質量定義得 
關鍵在相對論質量定義等價於  ,請看推導過程如下 1~7 :
,請看推導過程如下 1~7 :
- 由 定義5 得

- 兩邊都對 t 微分,由於
 和
和  都不會隨時間變化,對時間微分會得 0 ,所以
都不會隨時間變化,對時間微分會得 0 ,所以 
 ,化簡得
,化簡得 
- c 為常數,m、v均為變數,化簡上式得

- 用積分公式得

- 化簡上式得

- 三項同除以 2m 得

- 代入第①式得:

- 對其積分得相對論動能

渺子衰變
渺子壽命: 秒,從渺子誕生到衰變的平均運動距離是660公尺
秒,從渺子誕生到衰變的平均運動距離是660公尺
渺子在海平面15公里上空由宇宙線撞擊大氣分子而形成,照說 秒的生命只能走完660公尺。為什麼從地面卻可以測量到許多渺子?原因是渺子以接近光速的速度運動,所以渺子的時間會變慢,這是時間膨脹。因此從地面上的觀察者來看,渺子的壽命比2.2微秒還要長很多,足夠時間穿過15公里的大氣層到地面。
秒的生命只能走完660公尺。為什麼從地面卻可以測量到許多渺子?原因是渺子以接近光速的速度運動,所以渺子的時間會變慢,這是時間膨脹。因此從地面上的觀察者來看,渺子的壽命比2.2微秒還要長很多,足夠時間穿過15公里的大氣層到地面。
如果以渺子的角度來觀察的話,渺子是靜止不動的,反而是地球以光速朝渺子奔來,根據上面講的長度收縮,地球與渺子之間的距離縮短很多,所以渺子能在衰變之前就到達地面。
渺子的速度是0.9994光速。
- 時間由1秒膨脹到28.571秒:

- 0.9994光速為每秒29.982公里,時間膨脹到28.571秒
 (萬)
(萬)
 (萬萬)
(萬萬)- 光速還是接近於30萬公里:

時間彎曲
 時空彎曲
時空彎曲
- 有質量的物體都會形成重力場,質量越大,重力場越大。
- 愛因斯坦在1911年發表的廣義相對論,所講的就是重力(萬有引力)的本質是物體的分布彎曲了時空,所以宇宙中星體就會造成附近空間的彎曲,鄰近的物體接近就會陷進時空彎曲的範圍中,形成橢圓的軌道繞著那個星球,速度很慢的物體就會直接撞上去。
- 當物體以高速前進時,進入到時空彎曲範圍,他的行徑路線就會偏離。例如光,遙遠星球發出的光經過許多星球時值線軌道就會偏離,偏離的光只有極少數角度才會被我們觀測到。
- 太陽的質量讓整個太陽系時空彎曲,所以地球也以橢圓軌道繞著太陽運行。





















































