位移、速度與加速度

概述

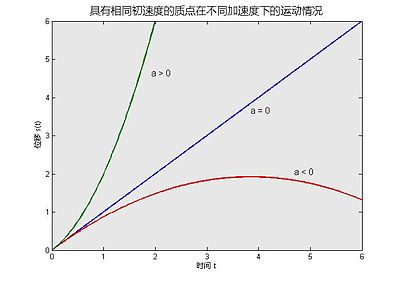位移-時間圖

三個質點從坐標原點以相同的速度出發，由於分別擁有正、零、負的加速度而導致其位置和關於時間的曲線。原公式分別為：

1. 綠線:s(t)=t²+t，加速度 a 與初速同方向，時間越往後，每單位時間所進行的位移越大。
2. 藍線:s(t)=t，加速度 a 為 0 ，任可時間其每單位時間的位移皆不變，即速度皆不變。
3. 紅線:s(t)=-0.13*t²+t，加速度 a 與初速相反方向，加速度會逐漸抵消掉初速，直到速度為 0 ，然後加速度會使質點的運動回頭，時間越往後回頭的速度越快，每單位時間「負向」位移越大。

藍線的幾何圖形是直線，綠線和紅線的幾何圖形是拋物線。綠線的最高次項係數為正值，所以右側向上；紅線的最高次項係數為負值，所以右側向下。

定義

加入方向考慮之後，如何從一段運動軌跡得到加速度。

1. 位移：物體位置的變化，包含零位移。
2. 速度：物體在單位時間內的位移。即位移對時間的微分。速度包含大小和方向兩個元素。其中「大小」叫做「速率」。但速度與「位置」無關，等速運動中，不管位置在哪裡，其速度不變，都是同一個值，因為其大小和方向皆相同。
3. 加速度：物體在單位時間內速度的變化。即速度對時間的微分。加速度也包含大小和方向兩個元素，也與位置無關。

右圖中綠線是運動的軌跡，藍線及箭頭(S₁、S₂、S₃…)代表每單位時間位移的向量。由小圖中可以看到 v₁=S₁/Δt , v₂=S₂/Δt ，而加速度 a₁=v₂-v₁/Δt 。

位移、速度與加速度是用來解釋微積分極好的工具，因為：

	三者在微積分上階層簡明：位移的微分得到速度，速度的微分得到加速度；而加速度的積分得到速度變化量，速度的積分得到位移。 三者用多項式就能表達。

圓周運動

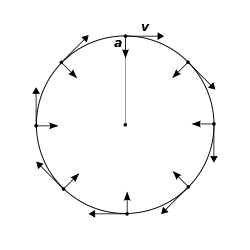
圖一:圓周運動切線速度與向心加速度示意圖

右圖紅色向量代表切線速度，不同瞬間，速率相等，速度不等(方向不同)。

藍色向量代表向心加速度，不同瞬間，加速度大小相等但方向不等。

注意，右圖中藍色向量的向心加速度標示過大，需要修改，真正的大小以圖二較為準確。

a,v,r 之間的大小關係

圖二:圓周運動 a,v,r 關係圖

1. $a={\frac {v_{2}-v_{1}}{\Delta {t}}}={\frac {\Delta {v}}{\Delta {t}}}$，必須與$r_{1}$平行且是$r_{1}$順時鐘轉180度
2. $v={\frac {r_{2}-r_{1}}{\Delta {t}}}={\frac {\Delta {r}}{\Delta {t}}}$
3. 求出 $a={\frac {v^{2}}{r}}$ 或 $ar=v^{2}$

證明：

圖二中右方與左方三角形相似 ${\frac {\Delta {v}}{v}}={\frac {\Delta {r}}{r}}$ =>

兩邊分母同乘 $\Delta {t}\quad {\frac {\Delta {v}}{v*\Delta {t}}}={\frac {\Delta {r}}{r*\Delta {t}}}$ =>

${\frac {1}{v}}*{\frac {\Delta {v}}{\Delta {t}}}={\frac {1}{r}}*{\frac {\Delta {r}}{\Delta {t}}}$ =>

${\frac {1}{v}}*a={\frac {1}{r}}*v$ =>

$a={\frac {v^{2}}{r}}$

圓周運動的動力過程

	有一個速度向量使運動軌跡直線前進
	加上與其垂直的加速度向量，因為加速度與原速度方向垂直，所以無法增加或抵消原速度的大小，只能改變其方向
	加速度將軌跡拉彎
	反覆上述的過程將得到一個圓周運動的軌跡

速度相加

A 在月台，看 B 在列車上，站在 A 的觀點：列車及 B 以速度 u 對他進行等速相對運動； B 在車上射出一發子彈(或光束)，此子彈(或光束)對 B 的相對速度為 v ，則此子彈(或光束)對 A 的相對速度為${\frac {u+v}{1+{\frac {u\times v}{c^{2}}}}}$或${\frac {u+v}{1+{\frac {u}{c}}\times {\frac {v}{c}}}}$，此公式特性如下：

1. 當 v 為 c 時，相加後的速度為 c 。也就是光束的速度不管從 A 或 B 的觀點來看都是 c 。
2. 速度相加後永遠小於等於 c 。
3. 當 u 、 v 都比 c 小很多時，相加後的速度趨近於 u+v 。

加速度與位移的關係

復習乘法公式

證明：$$

 
   
     
       a
     
   
   {\displaystyle a}
 

$a$為常數，當位移-時間關係為$$

 
   
     
       s
       =
       
         
           1
           2
         
       
       a
       
         t
         
           2
         
       
     
   
   {\displaystyle s={\frac {1}{2}}at^{2}}
 

$s={\frac {1}{2}}at^{2}$時，速度為$$

 
   
     
       a
       t
     
   
   {\displaystyle at}
 

$at$(此時稱為等加速度運動)

$s$代表不同時間物體的位置，和時間有以下關係：$s={\frac {1}{2}}at^{2}$即

1. $s(t)={\frac {1}{2}}at^{2}$
2. 稍早時間$t$的位置為$s_{1}={\frac {1}{2}}at^{2}$
3. 稍晚時間$t+\Delta t$的位置為$s_{2}={\frac {1}{2}}a(t+\Delta t)^{2}$
4. 在經過很短時間$\Delta t$的位置改變為$\Delta s=s_{2}-s_{1}$
5. $v={\frac {\Delta s}{\Delta t}}={\frac {s_{2}-s_{1}}{\Delta t}}={\frac {{\frac {1}{2}}a(t+\Delta t)^{2}-{\frac {1}{2}}at^{2}}{\Delta t}}={\frac {{\frac {1}{2}}a(t^{2}+2t\Delta t+\Delta t^{2})-{\frac {1}{2}}at^{2}}{\Delta t}}$

   $={\frac {{\frac {1}{2}}a(2t\Delta t+\Delta t^{2})}{\Delta t}}={\frac {at\Delta t+{\frac {1}{2}}a(\Delta t)^{2}}{\Delta t}}={\frac {at\Delta t}{\Delta t}}+{\frac {{\frac {1}{2}}a(\Delta t)(\Delta t)}{\Delta t}}=at+{\frac {1}{2}}a\Delta t$

   $\because {\frac {1}{2}}a\Delta t\to 0\therefore v=at$

切線斜率、微分、導數

設$y=f(x)$，則函式$f$在$a$點切線斜率、微分、導數、$f'(a)$、${\frac {dy}{dx}}$、${\frac {df(x)}{dx}}$、(${\frac {\Delta f(x)}{\Delta x}}$)、$\lim _{\Delta x\to 0}{\frac {f(a+\Delta x)-f(a)}{\Delta x}}$ 都代表同一個意思。

純量考量

同理，在只考純量的情形下：
設$s=f(t)$，則$v=f'(t)$而$a=f''(t)$

位移、速度與加速度的階層關係

f(x)， x 軸上有 a,b 兩點對應的函數值為 f(a) 與 f(b) ，f'(a) ~ f'(b) 函式曲線與 x 軸所夾面積，恰為 f(a) 與 f(b) 值的差；f''(a) ~ f''(b) 函式曲線與 x 軸所夾面積，恰為 f'(a) 與 f'(b) 值的差。

此關係是直接來自微積分的基本定義，所以對所有的微積分函式都成立。

第一個練習：等速運動

問題：等速運動，速度為2m/s，請作 1~10秒 的：

1. 位移-時間圖、表
2. 速度-時間圖、表
3. 加速度-時間圖、表

答： 將x軸設為時間

1. 位移-時間：位移y=2x
2. 速度-時間：速度y=2
3. 加速度-時間：加速度y=0

畫圖

1. x,y每單位取 30 點，每一單位畫一刻度：
   • 原點距左上角：0,400
   • 0~11 切 11 段

第二個練習：初速度為0，等加速度

問題：等加速度運動，初速度為 0 ，加速度為 0.2m/s²，請作 1~5秒 的：

1. 位移-時間圖、表
2. 速度-時間圖、表
3. 加速度-時間圖、表

答： 將x軸設為時間

1. 位移-時間：位移y=½(0.2)x²=0.1*x²
2. 速度-時間：速度y=(0.2)x=0.2*x
3. 加速度-時間：加速度y=0.2

畫圖

1. x,y每單位取 100 點，每一單位畫一刻度：
2. 原點距左上角：0,400
3. 0~6 切 6 段

第三個練習：速度與加速度同向

問題：等加速度運動，初速度為 1 ，加速度為 0.2m/s²，請作 1~5秒 的：

1. 位移-時間圖、表
2. 速度-時間圖、表
3. 加速度-時間圖、表

答： 將x軸設為時間

1. 位移-時間：位移y=½(0.2)x²+x=0.1*x²+x
2. 速度-時間：速度y=(0.2)x+1=0.2*x+1
3. 加速度-時間：加速度y=0.2

畫圖

1. x,y每單位取 100 點，每 0.1 單位畫一刻度：
2. 原點距左上角：0,400
3. 0~6 切 6 段

第四個練習：速度與加速度反向

問題：等加速度運動，初速度為 1 ，加速度為 -0.2m/s²，請作 1~10秒 的：

1. 位移-時間圖、表
2. 速度-時間圖、表
3. 加速度-時間圖、表

答：將x軸設為時間

1. 位移-時間：位移y=½(-0.2)x²+x=-0.1*x²+x
2. 速度-時間：速度y=(-0.2)x+1=-0.2*x+1
3. 加速度-時間：加速度y=-0.2

畫圖

1. x,y每單位取 100 點，每 0.1 單位畫一刻度
2. 原點距左上角：0,400
3. 各點之x值：始於0，終於11，切11段